Validierung der Grundlagen: RANS-Analyse
Mit einem weiteren Fall in unserer Reihe überprüfen wir erneut einige Grundlagen. Diesmal betrachten wir eine 2D-Mischschicht, um RANS-Turbulenzmodelle zu vergleichen.
Mit einem weiteren Fall in unserer Reihe überprüfen wir erneut einige Grundlagen. Diesmal betrachten wir eine 2D-Mischschicht, um RANS-Turbulenzmodelle zu vergleichen.
9 verschiedene RANS-Turbulenzmodelle werden in Siemens Simcenter STAR CCM+ 2020 unter Verwendung der Mischebenen-Daten aus der NACA-Datenbank verglichen. 7 dieser Modelle werden hinsichtlich der turbulenten kinetischen Energie verglichen, während alle 9 Modelle hinsichtlich der Geschwindigkeit verglichen werden. Die getesteten Modelle sind in der nachstehenden Liste zusammengefasst. Modelle mit einem * werden sowohl hinsichtlich der Geschwindigkeit als auch der turbulenten kinetischen Energie verglichen.
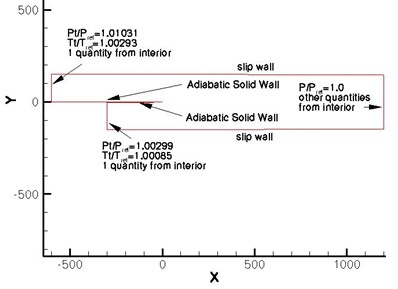
Die (2D-)Geometrie besteht aus zwei Einlässen mit zwei Geschwindigkeiten (der obere Einlass hat eine Geschwindigkeit von 41,54 m/s, der untere Einlass eine Geschwindigkeit von 22,4 m/s). Der obere Einlasskanal ist länger als der untere Einlasskanal. Eine Ebene trennt den oberen und den unteren Einlasskanal bis x = 0. Die Platte hat eine Dicke von 3 mm und ist auf den letzten 50 mm auf eine Dicke von 0,3 mm verjüngt. Diese Geometrie ist dieselbe wie die in der Referenz verwendete Geometrie, siehe die folgende Abbildung [1].
Die Referenztemperatur, Tref, beträgt 293 K, die Schallgeschwindigkeit, aref, 343 m/s und der Referenzdruck, Pref, beträgt 101325 Pa. Die Turbulenz in der freien Strömung wird mit 0,3 % angesetzt.
Da Femto bei der Arbeit mit CFD-Problemen normalerweise unstrukturierte Vernetzungen verwendet, wird für dieses Problem eine unstrukturierte Vernetzung eingesetzt. Es wird eine maximale Zellengröße von 10 mm verwendet. Die Nachlaufströmung der Splitterplatte wird mit Hilfe von Netz-Zellen mit einer Größe von 1,25 mm verfeinert.
Es werden Prismenschichten verwendet, um den y+-Wert an den Wänden auf <1 zu bringen.

In Abbildung 1 ist das Geschwindigkeitsprofil im Abstand von 200 mm von der Splitterplatte dargestellt. Der y-Wert ist mit der Wirbelstärke δω normiert, die mit der folgenden Gleichung berechnet wird.
In Abbildung 1 ist das Geschwindigkeitsprofil im Abstand von 200 mm von der Splitterplatte dargestellt. Der y-Wert ist mit der Wirbelstärke δ_ω normiert, die mit der folgenden Gleichung berechnet wird.
δ_ω=(U_2-U_1)/(δU/δy)
Die y-Werte werden anhand der Gleichung ycorrected=y-0.00688xkorrigiert. Schließlich wird auch die Geschwindigkeit anhand der folgenden Gleichung normalisiert.
Unorm=(U-U_1)/ΔU
Die Ergebnisse der CFD-Berechnungen werden mit experimentellen Daten verglichen [2].
Alle Turbulenzmodelle zeigen eine gute Übereinstimmung mit der experimentellen Geschwindigkeit bei x = 200 mm. Das realistische k-ε Modell sagt die Geschwindigkeitsänderung zwischen -0.2>y/δ_ω >-0.6 am besten voraus. Die anderen Modelle, die diese Geschwindigkeitsänderung ebenfalls vorhersagen, sind das High Re SA-Modell, das SST k-ω-Modell, das Standard k-ε-Modell und das realistische k-ε-Zweischichtmodell. Die anderen Modelle sagen keine plötzliche Änderung der Geschwindigkeit voraus.
Keines der 9 Turbulenzmodelle liefert eine genaue Vorhersage des Geschwindigkeitsprofils bei x = 650 mm (Abbildung 2). Die Modelle, die den experimentellen Daten am nächsten kommen, sind das Standard-k-ω-Modell und das quadratische Reynolds-Spannungsmodell.
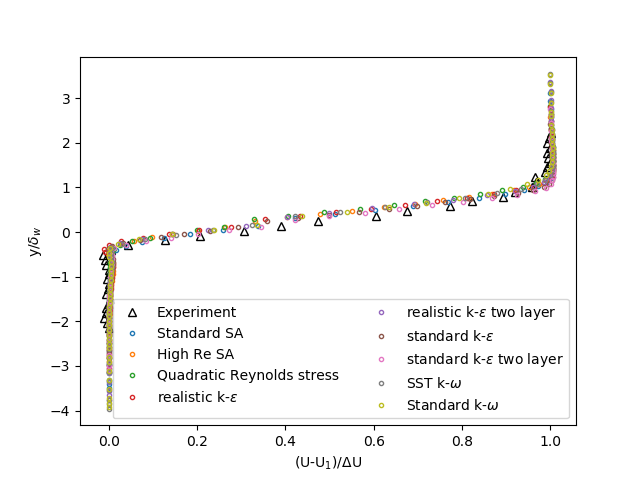
Abbildung 1: Geschwindigkeitsprofil bei x = 200 mm
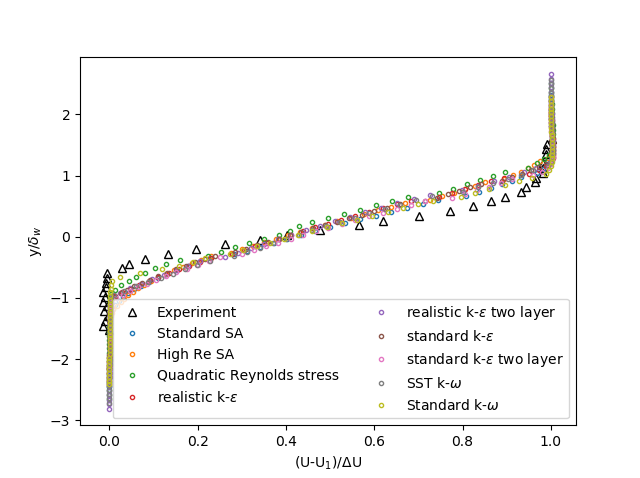
Abbildung 2: Geschwindigkeitsprofil bei x = 650mm
Die turbulente kinetische Energie wird mit der Quadratwurzel aus der Geschwindigkeitsdifferenz normiert. Da die beiden Spalart-Allmaras-Modelle (SA) keine turbulente kinetische Energie ausgeben, werden diese Modelle nicht für die turbulente kinetische Energie verglichen.
In Abbildung 3 wird die turbulente kinetische Energie bei x = 200 mm der 7 Turbulenzmodelle mit den experimentellen Daten verglichen. In dieser Abbildung ist zu erkennen, dass keines der Modelle den Punkt genau vorhersagt, an dem die turbulente kinetische Energie zu steigen beginnt. Die maximale turbulente kinetische Energie wird am ehesten von den Modellen Standard k-ω, SST k-ω und dem realistischen k-ε-Zweischichtmodell vorhergesagt. Die maximale kinetische Energie, die durch das quadratische Reynolds-Spannungsmodell vorhergesagt wird, ist ähnlich wie bei den anderen drei Modellen, aber die Position in y ist falsch. Die anderen drei Modelle sagen eine maximale turbulente kinetische Energie voraus, die viel höher ist als die der Experimente.
In Abbildung 4 ist die turbulente kinetische Energie bei x = 650 mm dargestellt. In diesem Fall wird das Verhalten der turbulenten kinetischen Energie am besten durch das Standard-k-ε und das realistische k-ε Modell vorhergesagt, sowohl in der Breite als auch in der Höhe. Die anderen Modelle sagen einen zu niedrigen Maximalwert der turbulenten kinetischen Energie und/oder einen zu frühen y-Wert voraus, bei dem die turbulente kinetische Energie zu steigen beginnt.
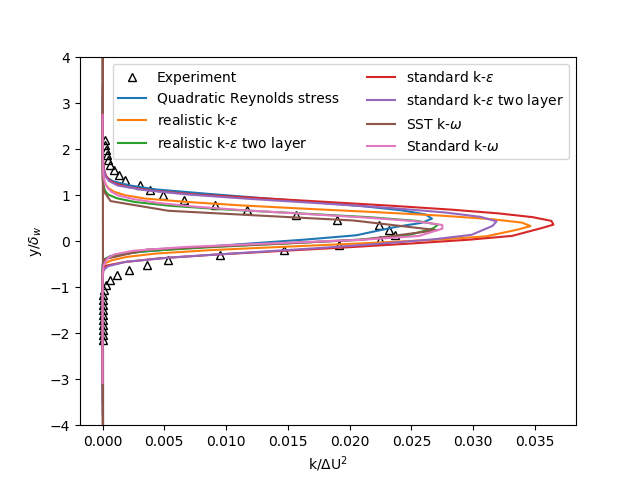
Abbildung 3: Turbulente kinetische Energie bei x = 200mm
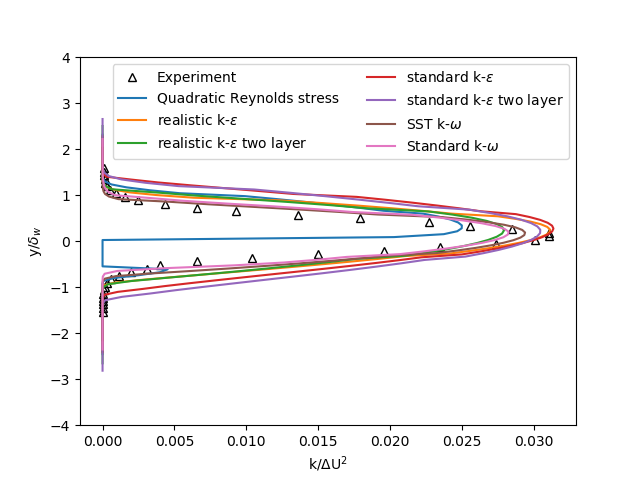
Abbildung 4: Turbulente kinetische Energie bei x = 650mm
We have a team of professionals with extensive knowledge that are happy to help. For any questions, use the form below to get in contact.
Benötigen Sie Information oder möchten Sie mit uns über Ihr Projekt sprechen? Nehmen Sie jeder Zeit Kontakt zu uns auf, gerne beantworten wir alle Ihre Fragen.
Bei Femto Engineering unterstützen wir Firmen dabei, ihre innovativen Projekte zu verwirklichen: mit Engineering, Produktentwicklung, Software, Training, Support und F&E. Wir sind in den Benelux Ländern lizensierter Händler für Simcenter Femap, Simcenter Simcenter 3D, Simcenter Nastran, Simcenter Amesim, Simcenter STAR-CCM+ und SDC Verifier. Melden Sie sich bei uns und lassen Sie die FEM und CFD Tools für sich arbeiten.
Melden Sie sich für unseren Newsletter an, um kostenlose Ressourcen, News und Updates monatlich in Ihrem Posteingang zu erhalten. Teilen Sie unser Fachwissen!