Festigkeitsberechnungen nach der Finite-Elemente-Methode
Theorie, Praxis und Software für Festigkeitsberechnungen
Theorie, Praxis und Software für Festigkeitsberechnungen
Mit diesem Artikel möchten wir Ihnen auf anschauliche Art und Weise linear statische Festigkeitsberechnungen mit der Finite-Elemente-Methode vorstellen. Mithilfe einer FEM-Software (oder 3D-Berechnungssoftware, EEM-, FEM- und Simulationssoftware) können solche Berechnungen durchgeführt werden, ohne ein tieferes Wissen über die zugrunde liegende Mathematik zu haben. Auch wenn Sie schnell anfangen möchten, ist ein gewisses Maß an Hintergrundwissen erforderlich, um Ergebnisse richtig zu interpretieren, sowie Fehler zu vermeiden und Probleme zu beheben. Deshalb tauchen wir im ersten Teil dieses Artikels in die Finite-Elemente-Methode ein. Im zweiten Teil dieses Artikels werden wir die Praxis, Anwendungen und Software diskutieren.
Das Prinzip der Finite-Elemente-Methode besteht darin, eine komplizierte Form in eine endliche Anzahl kleiner Bereiche zu unterteilen, die jeweils durch einfache Differentialgleichungen beschrieben werden können. Die Kombination dieser Differentialgleichungen führt zu einem Gleichungssystem, das bei seiner Lösung das Verhalten der gesamten Form beschreibt.
Beginnen wollen wir mit der Tatsache, dass in dem Bereich der Festigkeitslehre im Laufe der Zeit viele Methoden und Formeln entwickelt wurden, um die Festigkeit/Steifigkeit einer Struktur zu ermitteln. Die Finite-Elemente-Methode ist eine von Ihnen. Um die Funktionsweise dieser Methode zu veranschaulichen, verwenden wir das Beispiel einer Brücke. Falls Sie eine Brücke planen, wollen Sie frühzeitig wissen, wie sich die Kräfte, ausgelöst durch Verkehr oder Wind, auf Ihre Konstruktion auswirken. Allgemein gilt: Ein Gegenstand verändert seine Form, wenn Sie mit ausreichender Kraft an ihm ziehen oder Druck auf ihn ausüben.
Wie sehr sich die Form verändert, ist davon abhängig, aus welchem Material der Gegenstand besteht, welche Abmessungen er hat und wie groß die Kräfte sind. Im Falle eines einfachen Stabs reicht dann eine einzelne Differentialgleichung aus, um bei den gegebenen Informationen die resultierende Verformung des Stabs zu ermitteln. Bei einer Brücke handelt es sich jedoch um eine weitaus komplexere Form,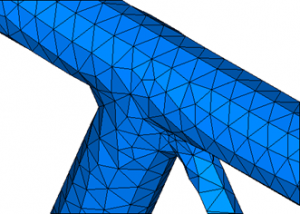
die sich nicht mehr durch eine Differentialgleichung beschreiben lässt. An diesem Punkt setzt der Grundgedanke der Finite-Elemente-Methode an: Eine komplexe Form wird in eine endliche (finite) Anzahl von einfachen Elementen zerlegt. Es entsteht ein Netz aus Elementen, die mittels Knoten miteinandern verbunden werden und die so ursprüngliche Form der Brücke wiedergeben. Einer der ersten Schriftte bei der Finite-Elemente-Methode ist die Erzeugung diese Netzes. Dazu muss zunächst eine Entscheidung getroffen werden, welche Art von Elementen dafür verwendet werden kann.
Ein Grundsatz bei der Wahl des geeigneten Elementtyps: Vernetzen Sie einen Bereich mit dem Elementtyp, der der ursprünglichen Geometrie am nächsten kommt. Für ein dünnes Blech eignen sich beispielsweise Platten- oder Schalenelemente häufig am besten. Klicken Sie hier, um eine Entscheidungshilfe für Ihre Wahl zwischen 1D- (Länge), 2D- (Fläche) oder 3D-Elementen (Volumen) zu erhalten. In dem folgenden Dokument finden Sie zudem einen praktischen Überblick darüber, wie sich die verschiedenen Elementtypen, die Größe und die Anzahl von Elementen auf die Qualität der Ergebnisse auswirken. Im mathematischen Sinn steht hinter jedem Elementtyp eine bestimmte Interpolationsfunktion, in der FEM auch Formfunktion genannt. Die Formfunktion bestimmt darüber, wie Spannungen und Verschiebungen innerhalb eines Elements auf die Knoten verteilt werden. Bei der Nutzung einer FEM-Software wird die Formfunktion durch die Wahl eines Elementtyps ausgewäht. Die Elementtypen unterscheiden sich nicht nur hinsichtlich ihrer Dimension, sondern auch ob ein oder zwei Knoten pro Kante vorhanden sind (Elemente erster oder zweiter Ordnung) und durch weitere, teils spezielle Eigenschaften. Im nachfolgenden Bild finden Sie einige Grundtypen von Elementen:
Die Genauigkeit der Berechnungen hängt von der Anzahl an Elementen und den damit verbundenen Knoten ab. Umso kleiner die Elemente werden, desto mehr Elemente finden in einem Bereich platz und desto genauer werden die Ergebnisse. Gleichzeitig steigt mit einer größeren Zahl an Elementen jedoch auch die Rechenzeit an. Aus diesem Grund versuchen wir stets den optimalen Punkt zu finden, bei dem innerhalb einer angemessenen Zeit ein ausreichend genaues Ergebniss erzielt werden kann. An dieser Stelle möchten wir Ihnen zwei wichtige Tipps geben: Es kann sinnvoll sein, das Netz an einer Stelle lokal zu verfeinern und die Berechnung erneut durchzuführen, um zu überprüfen, ob die betrachteten Werte sich verändern. Außerdem können an lokalen (kritischen) Punkten oft manuelle Berechnungen durchgeführt werden, um die Plausibilität des Modells zu überprüfen.
Für das Beispiel der Brücke wählen wir ein Hexaederelement erster Ordnung (8 Knoten). Im Allgemeinen kann sich jeder Knoten sowohl horizontal als auch vertikal bewegen. Eine Ausnahme bilden die Knoten an der Außenseiten, da die Brücke nicht in der Luft schwebt, sondern an diesen Stellen mit der Umgebung verbunden ist. Diese Fixierung muss bei der Berechnung zwingend berücksichtigt werden, um die korrekte Darstellung des physikalischen Problems zu erhalten. Darüber hinaus müssen die mechanischen Eigenschaften des Materials definiert werden und die äußeren Kräfte (z.B. Verkehr, Wind) müssen auf die Struktur aufgetragen werden.
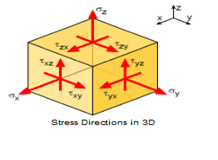
Wir beginnen mit der Grundbeziehung: Das Hooksche Gesetz besagt, dass die Dehnung Δl eines Festkörpers mit der Steifigkeit k linear von der wirkenden Kraft F abhängt (F = k * Δl). Außerdem lässt sich die Dehnung und damit die Verschiebung eines Knotens als Funktion von X- und Y-Koordinaten ausdrücken. Kombiniert man diese Beziehungen miteinander, erhält man eine Gleichung, die den Zusammenhang zwischen der auferlegten Kraft und der daraus resultierenden Verschiebung in X- und Y-Richtung beschreibt. Da jeder Knoten eine eigene Gleichung besitzt, ergibt sich für das Hexaenderelement in unserem Beispiel eine Matrix mit 8 Gleichungen. Wir nennen diese Matrix die Steifigkeitsmatrix eines Elementes, da in ihr die Materialeigenschaften enthalten sind.
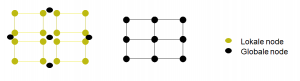Die Brücke soll nun aber nicht nur aus einem Element, sondern aus einer großen Zahl von Elementen bestehen. Da die Elemente über gemeinsame Knoten miteinander verbunden sind, wirkt sich die Verschiebung eines Elements auch auf alle anderen aus. Wir veranschaulichen das Prinzip der gemeinsamen Knoten hier anhand von Plattenelementen mit 4 Knoten.
Aufgrund dieser Verbindung untereinander können die einzelnen Steifigkeitsmatrizen der Elemente zu einer Gesamtsteifigkeitsmatrix kombiniert werden, die das mechanische Verhalten der gesamten Struktur beschreibt.
Kraft, Verschiebungsvektoren und Gesamtsteifigkeitsmatrix bilden ein lineares Gleichungssystem. Durch das Einbringen der Randbedingungen (z.B. Fixierung) wird das Gleichungssystem lösbar. Mittels einer Standardtechnik (Gaußverfahren) werden Teile der Matrix nach und nach eliminiert, was als Reduktion bezeichnet wird. Nach der vollständigen Reduktion ist die Verschiebung eines Knotens bekannt. Mithilfe der Lösung eines Knotens können nach und nach durch Einsetzen auch die Verschiebungen aller anderen Knoten errechnet werden. Aus der Verschiebung folgt nach dem Hookeschen Gesetz dann die Spannungsverteilung innerhalb des Netzes
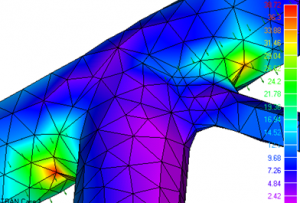Keine Sorge, Sie müssen keine Matrizen kombinieren oder Gleichungen lösen, denn das erledigt die FEM-Software für Sie. Auch die Darstellung der Ergebnisse, das Postprocessing genannt wird, übernimmt die Software und stellt die Spannungen in einem Konturdiagramm anschaulich dar.
In diesem Dokument finden Sie die wichtigsten Formeln zur Finite-Elemente-Analyse. Falls Sie weiterführende Informationen zum wissenschaftlichen Hintergrund von Festigkeitsberechnungen mit der Finite-Elemente-Methode wünschen, empfehlen wir Ihnen darüber hinaus diesen Artikel.
Bis jetzt haben wir über linear statische Berechnungen gesprochen und wie wir bereits erläutert haben, ist die Spannung in diesem Fall direkt proportional zur auferlegten Last. Dies gilt allerdings nur, wenn sich das Material rein elastisch verformt. Die sich ergebenden Verformungen sind deshalb auch nur vergleichsweise klein und haben somit auch keinen Einfluss auf das Verhalten der Struktur. Häufig stellen Berechnungen mit diesen Annahmen eine ausreichend gute Annäherung der realen Vorgänge dar. Kommt es allerdings zu großen Verformungen, was häufig bei Kunststoffen der Fall ist, oder geschehen andere nichtlineare Ereignisse, wie zum Beispiel Knicken oder Kontakt zwischen Teilen, dann sind nichtlineare Analysen erforderlich. Für nichtlineare Analysen sind mehr Eingangsdaten erforderlich und auch die Rechenzeit steigt oftmals um ein Vielfaches. Da auch die Bewertung der Ergebnisse weitaus schwieriger ist als bei linearen Festigkeitsberechnungen, erfordern nichtlineare Analysen in der Regel ein größeres Know-how.
Bevor FEM-Software entwickelt wurde, konnten Festigkeitsberechnungen ausschließlich von Hand durchgeführt werden. Dazu wurden mühsam Trägheits- und Widerstandsmomente ermittelt und darauf aufbauend konnten mit den Biegemomenten und Querkräften, die wiederum händisch errechnet werden mussten, die Spannungen an wenigen Stellen ermittelt werden. Moderne FEM-Software macht eine Vielzahl dieser Schritte parallel beim Aufbau des Modells, ohne dass für den Benutzer überhaupt erkennbar gerechnet wird. Erst bei der Ermittlung von anspruchsvolleren Ergebnissen wie der Von Mises-Spannungen oder den Eigenfrequenzen eines Systems wird dem Benutzer der Lösungsprozess ersichtlich. Durch die steigende Rechenleistung von Computern und die Weiterentwicklung der Software werden dabei nicht nur immer komplexere Probleme lösbar, sondern auch die Benutzerfreundlichkeit nimmt immer weiter zu, sodass diese Technik für Analysten, Ingenieure und Designer immer zugänglicher wird.
Die FEM-Softwarepakete bestehen in der Regel aus einem Pre- und Postprozessor und einem Solver. Mit einem Preprozessor bauen Sie das Modell auf und nehmen alle wichtigen Einstellungen für die Analyse vor. Der Solver ist vereinfacht gesagt der Gleichungslöser, der die eigentliche Berechnung durchführt. Der Postprozessor ermöglicht es anschließend, die Ergebnisse anschaulich zu visualisieren, damit so auch Nicht-Experten Einblick in die Ergebnisse bekommen.
Bei Femto verwenden wir Femap mit NX Nastran, Simcenter 3D und SDC Verifier, Abaqus und Optistruct zur Durchführung und zur Visualisierung unserer Analysen. Dieses Whitepaper gibt Ihnen einen Einblick in die Kriterien für eine erfolgreiche FEM-Pre- und Postprozessorauswahl.
Durch die allgemeine Formulierung der Theorie hinter der FEM kann mit einer modernen FEM-Software eine Vielzahl an physikalischen Effekten und Szenarios untersucht werden. In der Entwurfsphase können durch FEM-Simulationen Produkte und Konstruktionen so ausgelegt werden, dass sie den später auftretenden Belastungen standhalten. Gleichermaßen kann an manchen Stellen gezielt Material eingespart werden, wenn die Berechnungen niedrige Spannungen ergeben.
Die FEM-Software wird auch zur Überprüfung von Konstruktionen oder Produkten nach normierten Sicherheitsstandards eingesetzt. SDC Verifier ist ein Beispiel für ein FEM-Softwareprogramm, das speziell für diesen Zweck entwickelt wurde. Außerdem können FEM-Simulationen als Leitfaden bei dem Design eines Produktes dienen.
Wir nennen dies simulation-driven Design. Ein gutes Beispiel dafür ist die Topologieoptimierung. Aufgrund der steigenden Anforderungen an Sicherheit, der Reduzierung der Time-to-Market und dem Bedarf an Innovationen stellen wir fest, dass Simulationen immer häufiger eingesetzt werden. Eine interessante Entwicklung, die man im Auge behalten sollte, ist die des digitalen Zwillings.
Benötigen Sie Information oder möchten Sie mit uns über Ihr Projekt sprechen? Nehmen Sie jeder Zeit Kontakt zu uns auf, gerne beantworten wir alle Ihre Fragen.
Bei Femto Engineering unterstützen wir Firmen dabei, ihre innovativen Projekte zu verwirklichen: mit Engineering, Produktentwicklung, Software, Training, Support und F&E. Wir sind in den Benelux Ländern lizensierter Händler für Simcenter Femap, Simcenter Simcenter 3D, Simcenter Nastran, Simcenter Amesim, Simcenter STAR-CCM+ und SDC Verifier. Melden Sie sich bei uns und lassen Sie die FEM und CFD Tools für sich arbeiten.
Melden Sie sich für unseren Newsletter an, um kostenlose Ressourcen, News und Updates monatlich in Ihrem Posteingang zu erhalten. Teilen Sie unser Fachwissen!
