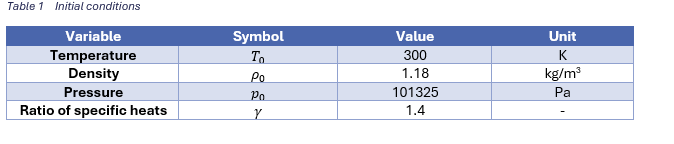
Ergebnisse
Das nachstehende Video gibt einen Einblick in die Funktionsweise des Overset-Netzes.
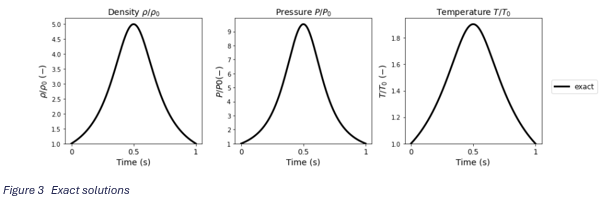
Es wird ein Vergleich zwischen der exakten Lösung und den Simulationsergebnissen angestellt. Die nachstehenden Diagramme zeigen die durchschnittliche Dichte, den Druck und die Temperatur im gesamten Gebiet für die verschiedenen Erhaltungseinstellungen des Overset-Netzes. Die exakte Lösung ist ebenfalls in den Diagrammen eingezeichnet.
Die in Abbildung 4 dargestellten Ergebnisse stammen aus Simulationen mit einem relativ großen Zeitschritt (dt = 0,01). Obwohl die Option der Massenverfolgung bessere Ergebnisse bei der Berechnung der Kompressionsraten liefert, ist eine leichte Verzögerung der Phasenverschiebung vorhanden. Wenn der Zeitschritt halbiert wird (dt = 0,005), verringert sich diese Phasenverschiebung. Dies ist in Abbildung 5 zu sehen. Die Ergebnisse für die anderen Maschenerhaltungseinstellungen verbessern sich ebenfalls, jedoch nicht ausreichend.
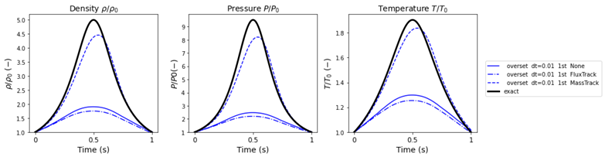
Figure 4 Results (with timestep: dt = 0.01)
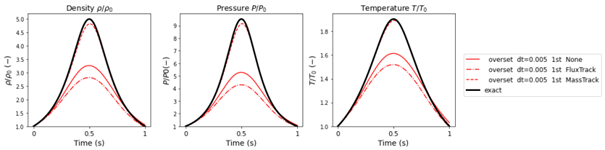
Figure 5 Results (with timestep: dt = 0.005)
The graphs clearly indicate that the results only come close to the exact solution when the mass tracking option is used. However, none of the overset conservation options provide a perfect solution. Interestingly, the flux tracking option does an even poorer job of conserving the mass during the simulation than having no overset conservation option at all.
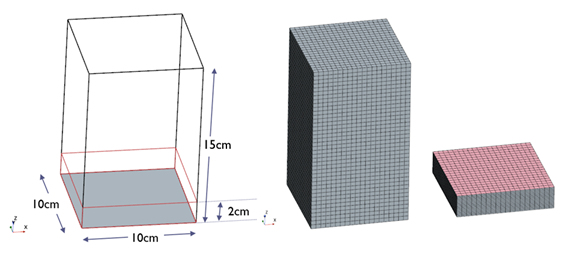
The reason for the poor performance of the flux correction has to do with the acceptor-to-active cells boundary. In an overset mesh the acceptor cell is a sort of “ghost cell” which receives information from all overlapping background mesh cells through the chosen interpolation scheme. The active cell then gets this information from the acceptor cell which is then used within the simulation. The flux correction enforces the mass flux through the acceptor-to-active cells boundary to be zero and implements this in the pressure-correction equation. This boundary is defined by the overset interface in the region and the number of zero-gap layers. In this case, this boundary is located 2cm above the valve surface, as shown in Figure 6.
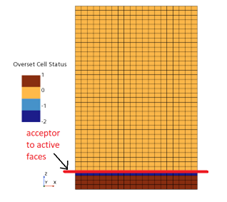
Abbildung 6 Grenze zwischen Akzeptor und aktiven Zellen
Technisch gesehen befindet sich eine Massensenke an dieser Grenze im Bereich 2 cm von der Ventiloberfläche entfernt. In Wirklichkeit sollte sich die Masse durch diese Flächen bewegen können. Eine Abhilfe könnte darin bestehen, die Übersatzfläche näher an die Ventiloberfläche zu bringen. Dies bedeutet jedoch auch, dass das Hintergrundnetz verfeinert werden muss, um eine ausreichende Anzahl von Zellen für die Anforderung der ZeroGap-Zellschicht zu erhalten. Die Dichte kehrt am Ende der Simulation zurück, was bedeutet, dass keine Masse verloren geht.
Im Gegensatz zur Flusskorrektur wirkt die Massenverfolgung eher wie eine Massenquelle als eine Senke. Diese Quelle wird in die Kontinuitätsgleichung aufgenommen. Dies ist anders als bei der Flusskorrektur, bei der die Druckkorrekturgleichung geändert wird. Die Massenverfolgung korrigiert die Masse zu einem bestimmten Zeitpunkt im Verhältnis zu der Menge an Masse, die ursprünglich im System vorhanden war. Der Unterschied in der Masse wird als Quellterm zur Kontinuitätsgleichung hinzugefügt.